A new type of pattern for aggregating bicycle frames allows for more adaptability.
Continue readingaggregation
Cluster 1: k-means optimization
Cluster 1: pattern use case speculations
Based on the specific potentials, we sketched potential use case scenarios for three different patterns.
Continue readingCluster 1: pattern malleability
Besides varying capabilities for adapting to form variation of constituent parts, the surface-based bike-frame aggregations we studied previously, also have different bending flexibility.
Continue readingCLUSTER 2: The Detergent Bottle as Building Block: From Geometry to Pattern to Surface Structure
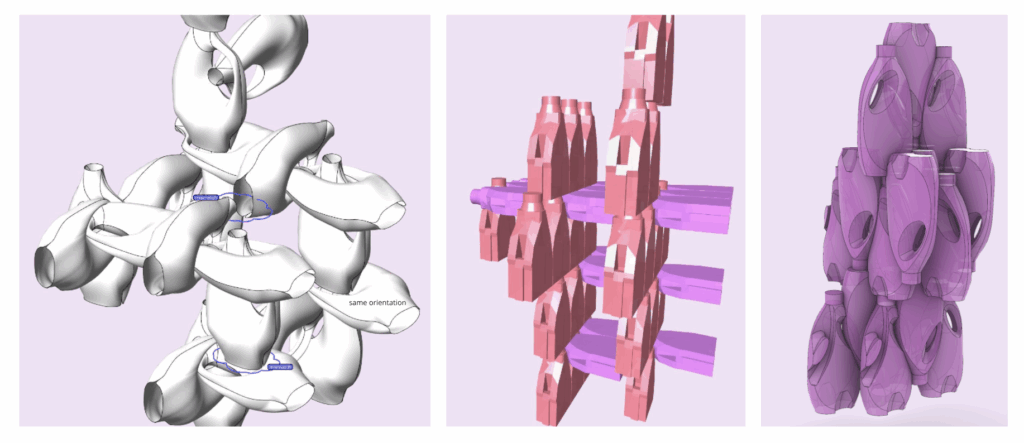
In this part of our ongoing exploration into how detergent bottles can become building blocks, we return to the idea of designing the shape of the bottle. Not by changing the form in complex ways, but by applying what we’ve learned from space-filling geometry.
Instead of completely transforming the bottle, we focused on minimal modifications, while making it suitable for a second life as a modular element.
CLUSTER 2: The Detergent Bottle as Building Block: Exploring Interlocking, Puzzle Logic, and Shape-Driven Reuse
Learning from the WOBO bottle – (you can read more in our previous blog post) – we were fascinated by how the design embedded reuse directly into the form of the packaging.
We’ve been exploring the idea of giving packaging not just a second life through recycling, but a second function through design. This led us to experiment with how detergent bottles could be transformed into interlocking, modular components, inspired by Japanese joinery, 3D puzzle logic.
CLUSTER 2: Learning from Heineken’s WOBO Bottle
WOBO: The Beer Bottle Designed to Build Homes. In the 1960s, Alfred Heineken visited Curaçao and noticed two things: beaches were littered with glass bottles, many from his own brand, and a huge housing shortage. This led him to an idea: what if beer bottles could be used as bricks for housing?
Continue readingCluster 3: Space Filling Geometry Systems – Approximating Artefacts Through Geometry
In this phase of the project, we’ve shifted our perspective. Until now, the physical experiments revolved around pressing artefacts into a predefined geometric mold. Specifically, we worked with the Peter Pearce’s Curved Space System, using saddle pentagons to form a continuous surface. This approach treated geometry as the fixed system, and artefacts as materials to be adapted. But what if we turned the concept around?
Continue readingCluster 3: Toy recreated- Curved Space Diamond Structure
We’ve recreated all five pieces of the Curved Space for 3D printing, transforming them into a toy. The goal was to explore the challenges and problems of the structure on a small scale in order to better understand what needs attention when scaling up.
Continue readingCluster 3 – Curved Space Diamond Structure Analysis
In an effort to advance discrete element aggregation using the Grasshopper3D plugin WASP (and Andrea building new features into it along the way), we are exploring a ‘sequence-based design’ approach and identified Peter Pearce’s Curved Space Diamond Structure as an ideal foundation.
