clustering of an inventory

| Daniela Kröhnert

Applying a clustering algorithm to an inventory of irregular unique objects can help to reduce the complexity involved in designing with such parts significantly. By dividing the inventory items into groups with similar characteristics, each group can then be represented by one “proto-part” instead, therefore reducing the amount of unique elements to be handled in setting up aggregation logics and the aggregation processes.
The decision about the number of different groups (Fig. 1) can be completely left to an algorithm (depending on various predefined – by the programmer – conditions) or be manually determined by the user/designer.

Fig. 1: clustering of inventory with different amounts of groups (“proto-parts”)

Furthermore, the reduction to a certain amount of groups allows training of an AI-model (future blog post), that will be able to continually produce aggregations from the representing “proto-parts” (Figs. 2 + 3); instead of the need of a new training phase for each new set of parts – as long as each new part fits in one of the initial groups of the training set.

Fig. 2 and 3: two topologically equal aggregations with different arrangements of “proto-parts” representing all the available parts from a possible inventory

Especially in an industrial product lifecycle1 this offers a lot of potential as most products’ geometric variance and structural potential tends to fall within a very limited range, due to norms and regulations and fabrication (mass production) constraints. For industrial artifacts it is much easier to find a smaller/limited representative set of “proto-parts” with lesser variance of the individual parts to their “proto-part” than for example in natural materials like tree branches (Fig. 4) or crushed rocks.

Fig. 4: A set of 42 tree branch forks grouped into 5 clusters. A much larger variance between the individual items within the same cluster are visible, especially when compared to industrial objects like e.g. bike-frames (see Fig.1)

In the course of the preceeding research project Conceptual Joining we assembled spacial frameworks made of beechwood branch forks and used one single “proto-branch” for the initial set up which then got populated with the actual items from the sets of branch forks. This led to significantly different grid spacings between the different prototypes (Fig. 5).

Fig. 5: The topologically equal grids from two different “proto-parts”. The proto-part used in the left hand grid is generated from a set of branch forks with much larger crotch angles than the right hand one. (www.conceptual-joining.com)

Replacing the proto-parts with the geometry of the actual parts will then change the global form of the structure. That means the form of the initial aggregation will change during the replacement with the actual parts depending on how close the approximated proto-part is or on how many different proto-parts are used for its generation.

Having the ability to adjust the amount of representative proto-parts to design with provides flexibility and designerly freedom to choose from the complete range between a set of unique elements to one single proto-part. The complexity of setting up aggregation logics can be adjusted in relation to i.a. the type of artifacts in use or the skill-level of the designer.

K-means Clustering

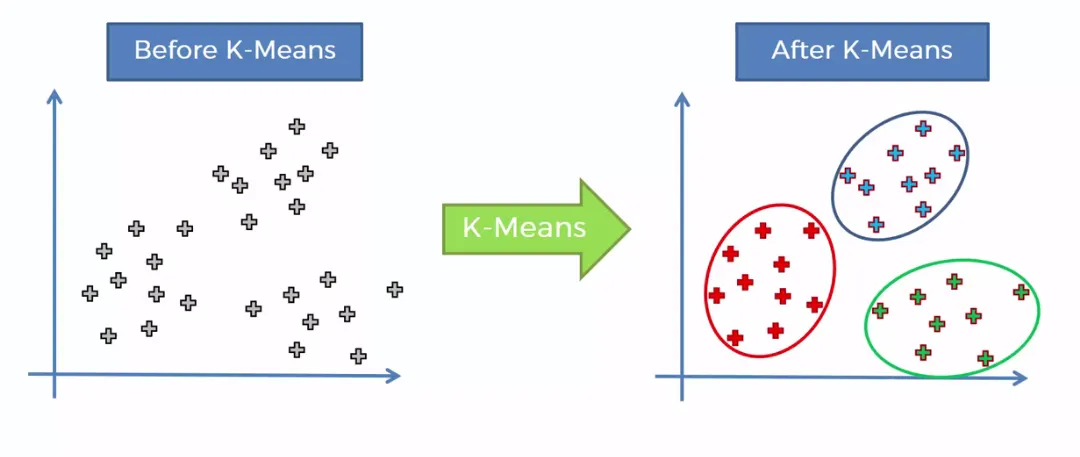
Fig. 6: “K-means uses an iterative refinement method to produce its final clustering based on the number of clusters defined by the user (represented by the variable K) and the dataset. It tries to make the data points of same cluster as similar as possible while also keeping the clusters as different as possible.“2

Based on an implementation by Andrea Rossi of the K-means clustering method from the previous project Conceptual Joining the first step was to implement the K-means++ initialization, a smarter initialization method, which spreads out the initial cluster centers more evenly.

Regular K-means Initialization

  1. Random Initialization:
    • The standard kMeans algorithm starts by randomly selecting k points from the dataset as the initial cluster centers.
    • This random initialization can sometimes result in poor clustering because the initial centers may not be representative of the actual distribution of the data.

K-means++ Initialization

  1. First Center Selection:
    • The first cluster center is chosen randomly from the data points.
  2. Subsequent Center Selection:
    • For each subsequent center, the algorithm does not just pick a point at random. Instead, it selects the next center with a probability proportional to the squared distance of the point from the nearest existing center.
    • Specifically, for each point x, calculate the distance D(x) to the nearest current cluster center.
    • Choose a new data point as a new center with probability proportional to D(x)^2.
  3. Iteration:
    • This process continues until all k centers have been chosen.

Implementing the K-means++ initialization solved a previously frequently reoccuring problem of the script generating wrong proto-parts – caused by some interations of the randomly choosen initial cluster centers – with no assigned items to their group (Fig. 7). With the K-means ++ features that error is completely resolved. (Fig. 8) Both illustrated with the branch fork dataset of the Conceptual Joining research project.

Fig. 7: Faulty proto-part generation with regular K-means clustering
Fig. 8: Proto-part and group generation with K-means++ clustering

With this implementation an experienced designer can already explore options and test out a range of cluster amounts to find a suitable one. However for a less exprienced user it might be reasonable to automate the determination of the number of clusters. According to ChatGPT the most common option includes the Elbow Method, a Variance Threshold or a Distance-based Threshold.

Implementing the Elbow Method

The elbow method is used to determine the optimal number of clusters (k) for a dataset. It computes the inertia (or within-cluster sum of squares) for different values of k. The optimal number of clusters is often identified at the “elbow point,” where the rate of inertia decrease slows down significantly.
These of course adds a lot of computing time to the script (in our Grasshopper3d definition from 1.3 seconds to 11.4 seconds for a maximum amount of 10 clusters and 50 iterations) as it has to calculate a range of number of clusters and then chooses the value where increasing the number of clusters does no longer significantly decreases the within-cluster sum of squares. (Fig. 9)

Fig. 9: Graphical representation of the Elbow Method3

The results are consistent with both data sets. With equal settings, no matter which first random cluster center is choosen for the K-means++ calculation the resulting optimum is always 2 clusters for the branch fork data set (42 items) (Fig. 10) and in the other very small bike-frame data set (18 items), depending on which bike is choosen as the first cluster center, the calculated optimum is either 2 (10 times) or 3 (8 times) (Fig.11).

Fig. 10: K-means clustering with elbow method for branch fork data set.
Fig. 11: K-means clustering with elbow method for bike-frame data set. First cluster center seen in the upper left corner, the resulting proto-parts below on the left side.

Integrating the Elbow Method reduces the amount of proto-parts drastically. In the case of small data sets like the bike-frames it also seems to not be consistent and the amount varies according to the first bike-frame that is choosen as the first cluster center. In contrast the branch fork dataset clustering does not vary that extremely depending on the first choosen brach fork and the generated proto-branches are consistent throughout all 42 possibilities. Although the clustering into two different groups is consistent, the visual difference between the individual items in each group is immense. It stands to reason that in at least such a case (organic artifacts) a larger number of clusters would possibly make more sense for an approach where the artifact is given more agency and becomes the driver for the global design.
However, further studies and larger data sets are needed to be able to come to serious conclusions.

Other aspects to invetigate further are different methods like the before mentioned Variance Threshold or Distance-based Threshold as a closer look at the intertias reveals that there might be a better “Elbow Point” where the amount of clusters is not minimized but a compromise between complete uniqueness and pure monotony. Here each proto-part would resemble its cluster’s items very closely and the designer would be relieved of some of the complexity instead of working with an inventory of unique parts. (Fig. 12)

Fig. 12: The curve shows the calculated intertias on Y for 1-10 clusters along X. The Elbow Method reduces the amount of generated proto-parts to an absolute mathematical minimum. Increasing the amount clusters by a reasonable amount still decreases the complexity for the designer but gives more agency to the artifacts (and the designer).
  1. McDonough, W. and Braungart, M. (2002) Cradle to cradle : remaking the way we make things. 1. ed.. New York, NY. ↩︎
  2. from https://medium.com/@pranav3nov/understanding-k-means-clustering-f5e2e84d2129 (last access September 10th 2024) ↩︎
  3. from https://medium.com/@zalarushirajsinh07/the-elbow-method-finding-the-optimal-number-of-clusters-d297f5aeb189 ((last access September 10th 2024)) ↩︎

The final python 2.7 code for Grasshopper3d / Rhino 7

import math
import random as rnd
import Grasshopper as gh
import ghpythonlib.treehelpers as th

# Remapping values from a source domain to a new target domain
def translate(value, sourceMin, sourceMax, targetMin, targetMax):
    sourceSpan = sourceMax - sourceMin
    targetSpan = targetMax - targetMin
    valueScaled = float(value - sourceMin) / float(sourceSpan)
    return targetMin + (valueScaled * targetSpan)

# Mapping the input values into a target domain 0-1
def normalize_values(lst, min_val, max_val):
    return [[translate(value, min_val, max_val, 0, 1) for value in sublist] for sublist in lst]

def vector_dist(v1, v2):
    distance = sum(math.pow(v2[i] - v1[i], 2) for i in range(len(v1)))
    return math.sqrt(distance)

def kMeansPlusPlusInitialization(vals, cls_num, first_center_index):
    cluster_centers = []
    first_center = vals[first_center_index]
    cluster_centers.append(first_center)
    
    for i in range(1, cls_num):
        distances = [min(vector_dist(val, center) for center in cluster_centers) for val in vals]
        total_distance = sum(distances)
        probabilities = [dist / total_distance for dist in distances]
        
        cumulative_probabilities = []
        cumulative_sum = 0
        for p in probabilities:
            cumulative_sum += p
            cumulative_probabilities.append(cumulative_sum)
        
        r = rnd.random()
        for i, cumulative_prob in enumerate(cumulative_probabilities):
            if r < cumulative_prob:
                cluster_centers.append(vals[i])
                break
    
    return cluster_centers

def kMeanClustering(vals, cls_num, iterations, first_center_index, min_val, max_val):
    # Normalize the input data
    norm_list = normalize_values(vals, min_val, max_val)

    cluster_centers = kMeansPlusPlusInitialization(norm_list, cls_num, first_center_index)
    
    for _ in range(iterations):
        clusters = [[] for _ in cluster_centers]
        clusters_ids = [[] for _ in cluster_centers]
        
        for i, norm_val in enumerate(norm_list):
            distances = [vector_dist(norm_val, center) for center in cluster_centers]
            best_center_id = distances.index(min(distances))
            
            clusters[best_center_id].append(norm_val)
            clusters_ids[best_center_id].append(i)
        
        for i, cluster in enumerate(clusters):
            if cluster:
                new_center = [sum(dim) / len(cluster) for dim in zip(*cluster)]
                cluster_centers[i] = new_center
            else:
                cluster_centers[i] = rnd.choice(norm_list)
    
    return th.list_to_tree(clusters_ids), cluster_centers

def compute_inertia(vals, cluster_ids, cluster_centers, min_val, max_val):
    inertia = 0
    cluster_ids_list = th.tree_to_list(cluster_ids)
    
    # Normalize the original values for distance computation
    norm_vals = normalize_values([list(val) for val in vals], min_val, max_val)
    
    for cluster_idx, cluster_branch in enumerate(cluster_ids_list):
        for point_idx in cluster_branch:
            inertia += vector_dist(norm_vals[point_idx], cluster_centers[cluster_idx]) ** 2
    return inertia

def elbow_method(vals, max_clusters, iterations, first_center_index, min_val, max_val):
    inertias = []
    first_centerindices = []
    for i in range(1, max_clusters + 1):
        cluster_ids, cluster_centers = kMeanClustering(vals, i, iterations, first_center_index, min_val, max_val)
        inertia = compute_inertia(vals, cluster_ids, cluster_centers, min_val, max_val)
        inertias.append(inertia)
        print("Number of clusters: {0}, Inertia: {1}".format(i, inertia))
    return inertias

def find_optimal_clusters(inertias):
    elbow_point = 0
    max_gradient = 0
    for i in range(1, len(inertias)):
        gradient = inertias[i - 1] - inertias[i]
        if gradient > max_gradient:
            max_gradient = gradient
            elbow_point = i
    return elbow_point + 1

# Main script
rnd.seed(2)

values = [[item for item in branch] for branch in value_tree.Branches]

# Compute min_val and max_val for the entire dataset
all_values = [item for sublist in values for item in sublist]
min_val = min(all_values)
max_val = max(all_values)

# Perform the elbow method to determine the optimal number of clusters
inertias = elbow_method(values, max_clusters, iterations, first_center_index, min_val, max_val)
optimal_clusters = find_optimal_clusters(inertias)

# Run the final clustering with the optimal number of clusters
ids, avg_norm_centers = kMeanClustering(values, optimal_clusters, iterations, first_center_index, min_val, max_val)

# Translate the normalized cluster centers back to the original domain
mapped_centers = []
for center in avg_norm_centers:
    mapped_center = [translate(center[i], 0, 1, min_val, max_val) for i in range(len(center))]
    mapped_centers.append(mapped_center)

# print("Cluster IDs:", ids)
# print("Cluster Centers (avg):", mapped_centers)

# Assign the output parameters
avg = th.list_to_tree(mapped_centers)
i = th.list_to_tree(inertias)