
We’re returning to the detergent bottle — and to the techniques we explored earlier with pressed plastic panels in the Pearse structure. But this time, the goal is to preserve more of the bottle’s original shape while still transforming it into a structural element.
Can we press parts of the bottle — but not all — and make use of the existing form, especially the necks and openings? Can we design a system that uses these bottles not just as raw material, but as functional nodes within a larger, repeatable geometry? Instead of randomly fusing plastic parts together, we’re asking: Can we build with minimal modification — and still end up with a system that’s modular, scalable, and structurally sound?

We started by preserving the necks and caps of HDPE detergent bottles, using them as connection points for pipes. The body of the bottles — particularly the flat base or midsection — was melted and pressed together to connect 2-6 bottels, allowing us to stable junctions without distorting the necks. These pressed-together “nodes” become the key units of construction.

The bottles remain recognizable, maintaining their original identity while gaining new structural purpose.
Self-Stabilizing Shape: Bucky Dome
We needed a shape that’s modular, repeatable, and self-stabilizing once closed. Naturally, we arrived at the geodesic dome — a structure made from interconnected triangles that distribute force evenly and curve naturally into a sphere.
But there’s a challenge with geodesic domes: they require multiple strut lengths and complex joints where up to six elements meet at a node. This isn’t ideal when working with reused and modular materials and aiming for simplicity.
Instead, we explored hexagon and pentagon domes. In a 3V frequency dome, triangles can be converted into hexagons and pentagons — simplifying the design. Each node now has only three pipes instead of five or six, and all the nodes are identical and can be repeatable.
Digital First: Simulating the System
Before jumping into physical prototypes, we recreated the concept in 3D. We modeled detergent bottles as nodes, connected by pipes of fixed length, and observed how the nods bend in the 3D space.

We explored the feasibility of the system, the curvature needed, For our current dome size, each triangle must bend about 11° per edge — a movement of around 5 cm in space. The digital simulation helped us validate that this should be physically achievable.
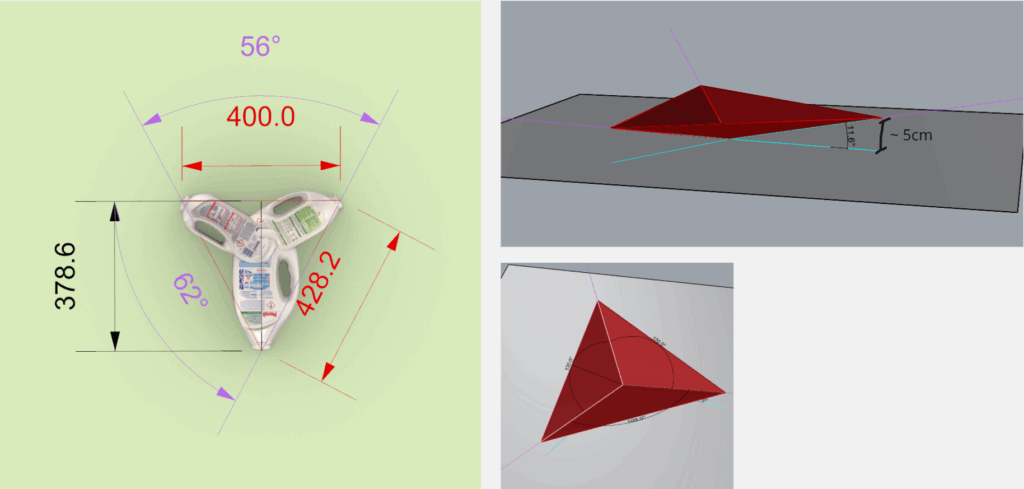
Physical Testing: Flat to Form
We moved to physical tests to see what actually works with real bottles.
This is also where the main strategy became clear:
Build the nodes flat — let the material and geometry do the shaping.

We heat and press the bottle bodies while keeping their necks intact, creating flat junctions. During assembly, the fixed-length pipes force these flat nodes to bend in space. This results in:
- A natural curvature of the structure
- Emergent geometric self-organization
- A system shaped not just by design, but by material behavior
In other words, the geometry becomes the shaping force — and HDPE’s flexibility makes it possible.
We tested two approaches:
- Cutting the bottle sides to press them more easily. It worked, but compromised the structural integrity.
- No cutting — just pressing intact bottles. This method preserved form stability, saved time, and kepta little bit more the bottle’s visual identity.

One Node as a Toolkit – Many Shapes
The long-term goal: create a single connection system that can form multiple structures. Could we use the same bottle node — plus 2–3 pipe lengths — to build domes, tunnels, cylinders, and more? A modular kit could adapt to different shapes — for now all digitally.
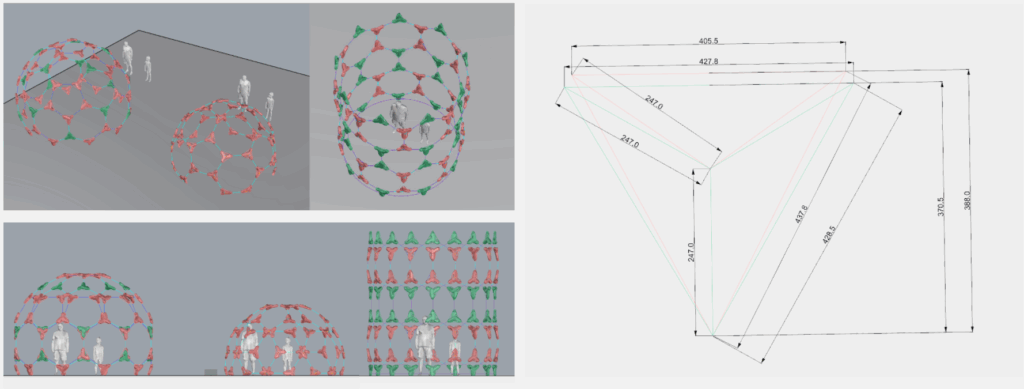
In digital experiments, we tested a larger geodesic dome and a cylindric shape that normally requires two types of nodes.( red and green) We found that the flexibility of the real material might allow us to use just one node design. Small differences in triangle shape should be tolerable — the physical system should absorb those variations.
What’s Next?
We’re now looking to define the limits of variation. How far can we push the nodes digitally before they no longer behave similarly in the real world? Finding that threshold means we can predict what other shapes — beyond domes — might be built with the same toolkit.