
In this phase of the project, we’ve shifted our perspective. Until now, the physical experiments revolved around pressing artefacts into a predefined geometric mold. Specifically, we worked with the Peter Pearce’s Curved Space System, using saddle pentagons to form a continuous surface. This approach treated geometry as the fixed system, and artefacts as materials to be adapted. But what if we turned the concept around?
Instead of shaping objects to fit into a system, we asked: Can a geometric system adapt to approximate an object? Could we create a discrete, modular logic that gets close enough to the artefact’s form so that the object itself becomes a functional element within the system?
Discovering Space-Filling Geometry Systems
The transition away from the Pearse system was driven by a practical limitation: its reliance on edge-to-edge connections. This type of connection required a high level of precision and didn’t allow room for variation or inaccuracy.
So we began looking at systems built from solid geometries, where the connection happens face to face rather than edge to edge.
This exploration quickly led us to space-filling systems—three-dimensional tilings that completely fill space using repeating solids, with no gaps or overlaps. All solids connect via full faces, and all connections are repeatable.
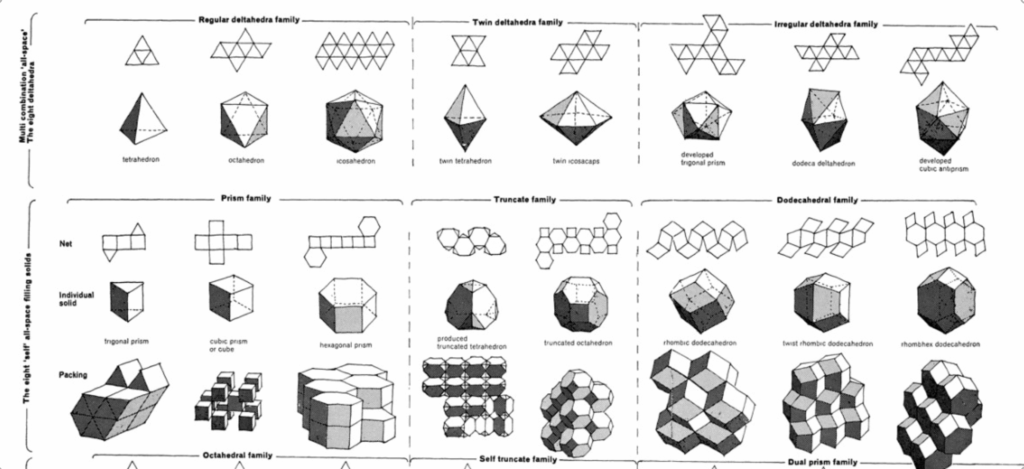
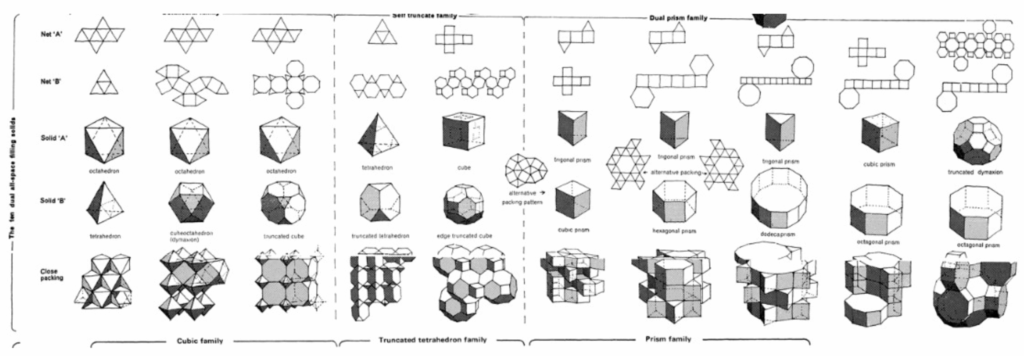
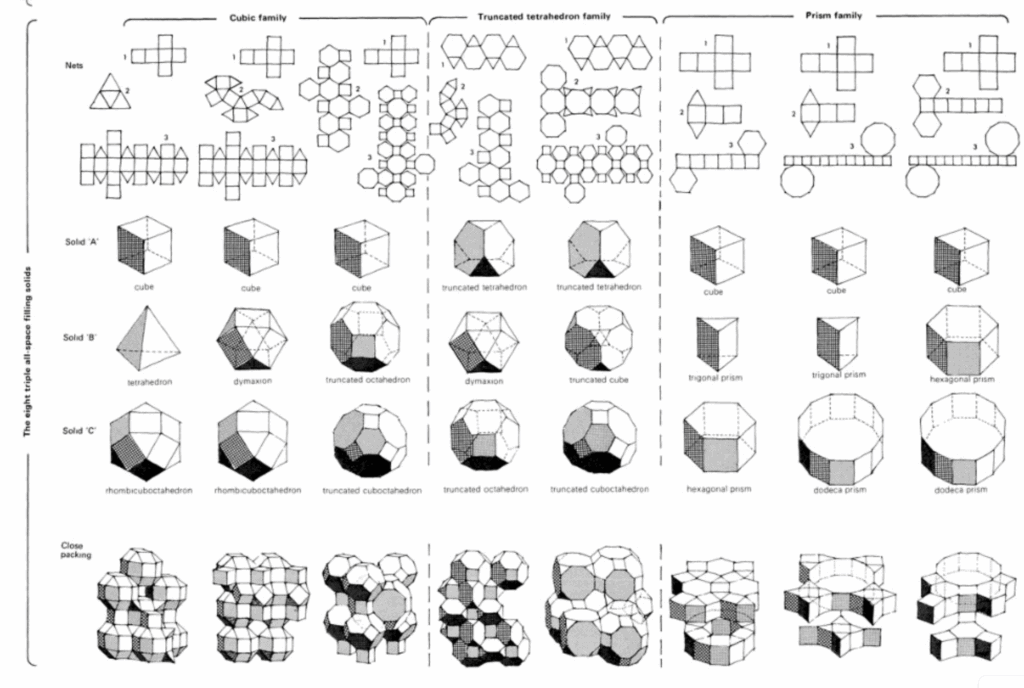
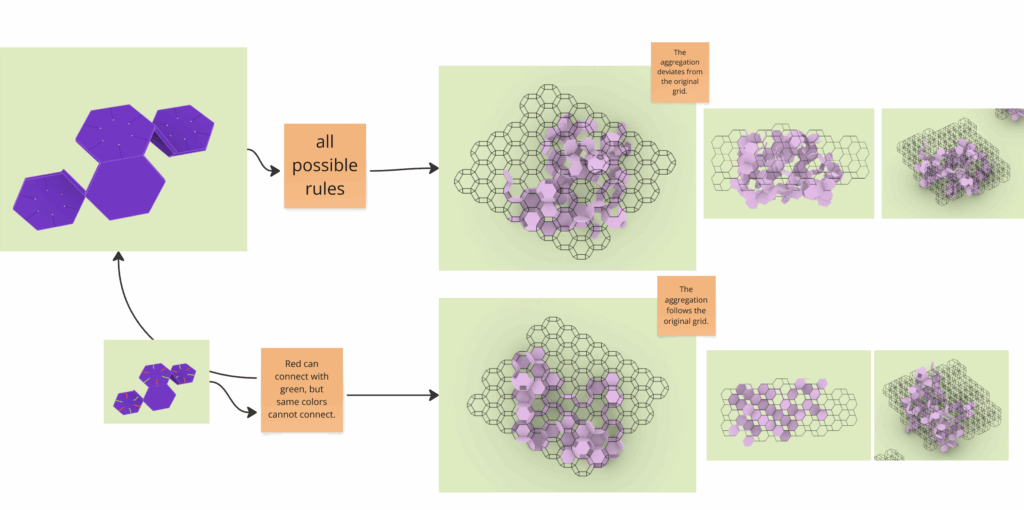
We began experimenting with these systems by extracting fragments—small modules made up of two to eight connected surfaces. These fragments became our new building blocks. Since they were originally part of a larger grid, they can be reassembled to fit back into that structure. By adding surface thickness, we avoided previous issues related to flatness and fragility.
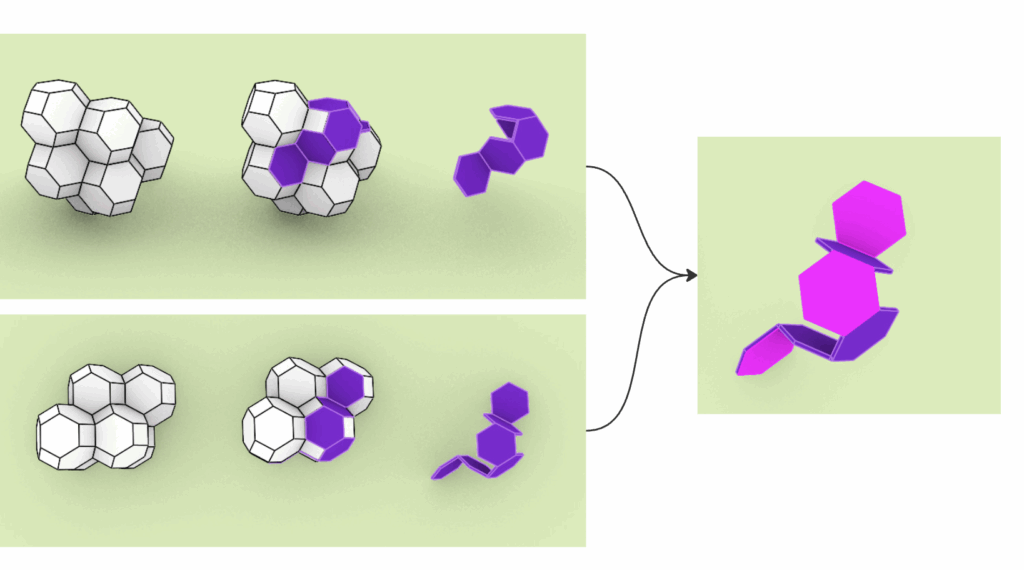
However, one condition was crucial: connections between these modules could only happen on the outside of the original solids. Attempting to connect surfaces that belonged inside the volume caused overlapping geometries and misalignments. This made it important to define clear rules for how and where parts could attach.
The way these modules connect affects the entire aggregation. If every surface is allowed to connect freely, the resulting structure deviates from the original grid logic. But if we impose limits—selecting only certain faces and orientations—the system retains a memory of its original pattern.
Approximation of Artefacts
With this system of modular fragments, the next challenge was to ask: Can we use these geometric systems to approximate the shape of an existing artefact?
We chose a detergent bottle as our first test object. To explore the approximation process, we developed a script in Grasshopper. The script generated a series of space-filling grids with scalable parameters and allowed us to place the artefact within them. From there, it analyzed each solid in the grid to find the surface most closely aligned with the artefact’s geometry. It identified surfaces with similar normal directions and minimal distance to the artefact’s mesh.
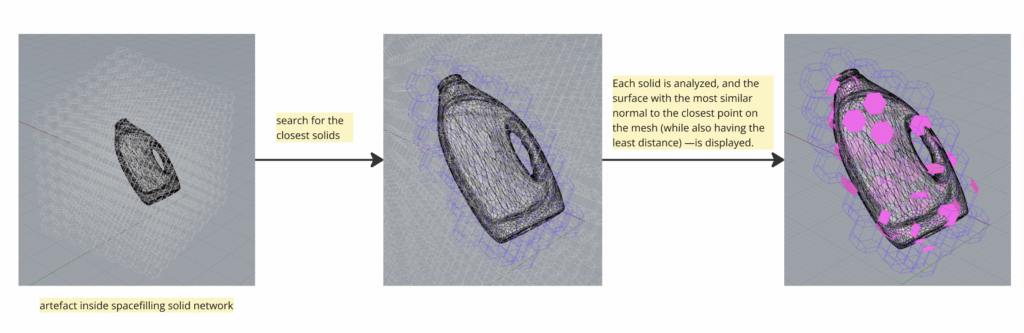
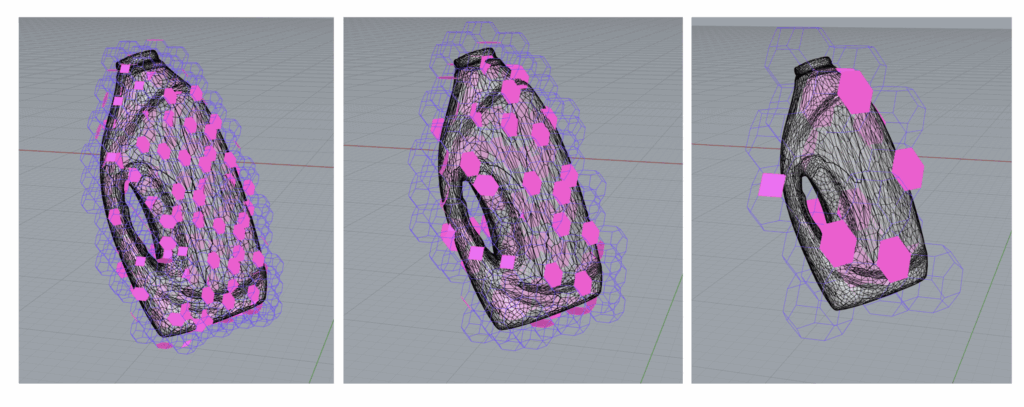
This process allowed us to experiment by rotating the object or scaling the grid to improve the fit. One big limitation was the geometric systems we used had a limited range of angles and directions—those defined by the inherent geometry of the solids within the grid. To approximate more complex or curved forms, we would need geometry systems with greater variability and richer surface language.

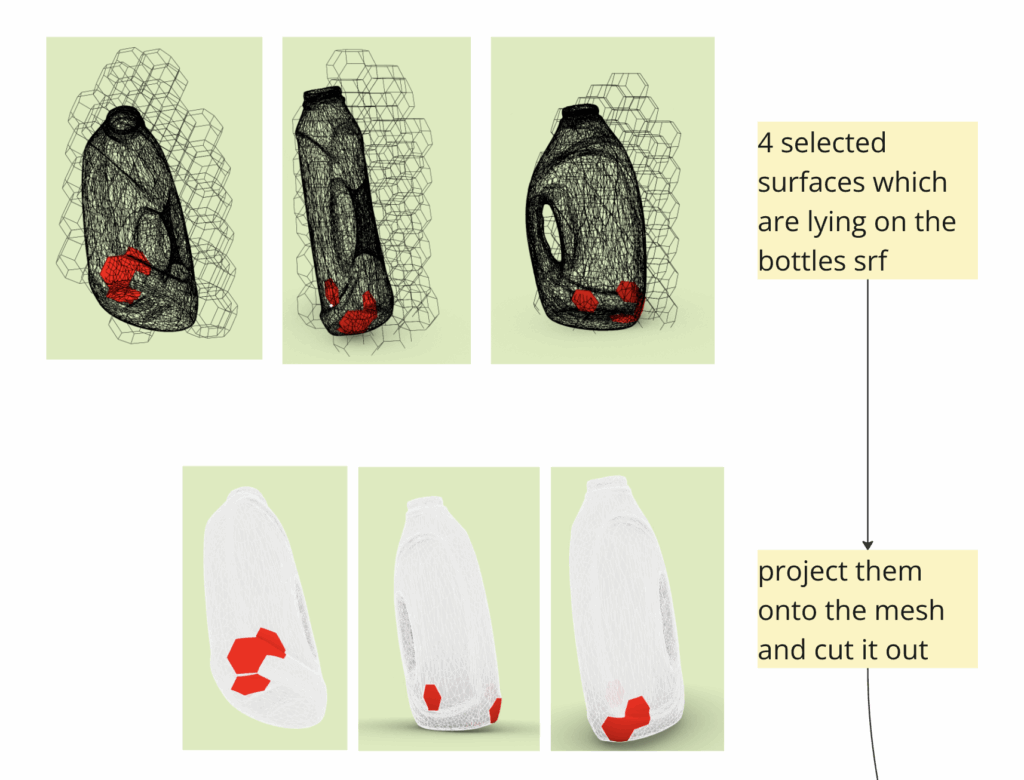
WORKFLOW: From Surface Fit to new Modules
Despite these limitations, we carried out a first proof-of-concept. We selected four surfaces from the detergent bottle that best matched the space-filling grid and projected them onto the bottle’s mesh. The resulting space between these four faces was closed with freely drawn surfaces, forming a complete part.
This “part” was then digitally cut out of the bottle and treated as a discrete module—complete with its four connection surfaces. When placed into Wasp, this part could now be aggregated into larger, stochastic structures. A small piece of waste was now embedded into a system of repeatable geometry. It no longer existed as a discarded object, but as an active part of a new geometric logic.


– but this raised a deeper question: Does it make sense to only reuse a small fragment of a waste object? What if we could integrate the entire artefact.
This led us to two strategies for fully incorporating the whole artefact into the system.
Integrating the Whole
The first strategy involves adding geometry to the artefact. Space-filling solids are positioned on its surface according to the logic of the grid, then 3D-printed directly onto it. The solids are added sparingly—just enough to allow aggregation—while still maintaining the grid’s order. These additions can form random or linear aggregations, and even loop-based sequences to build layered structures.
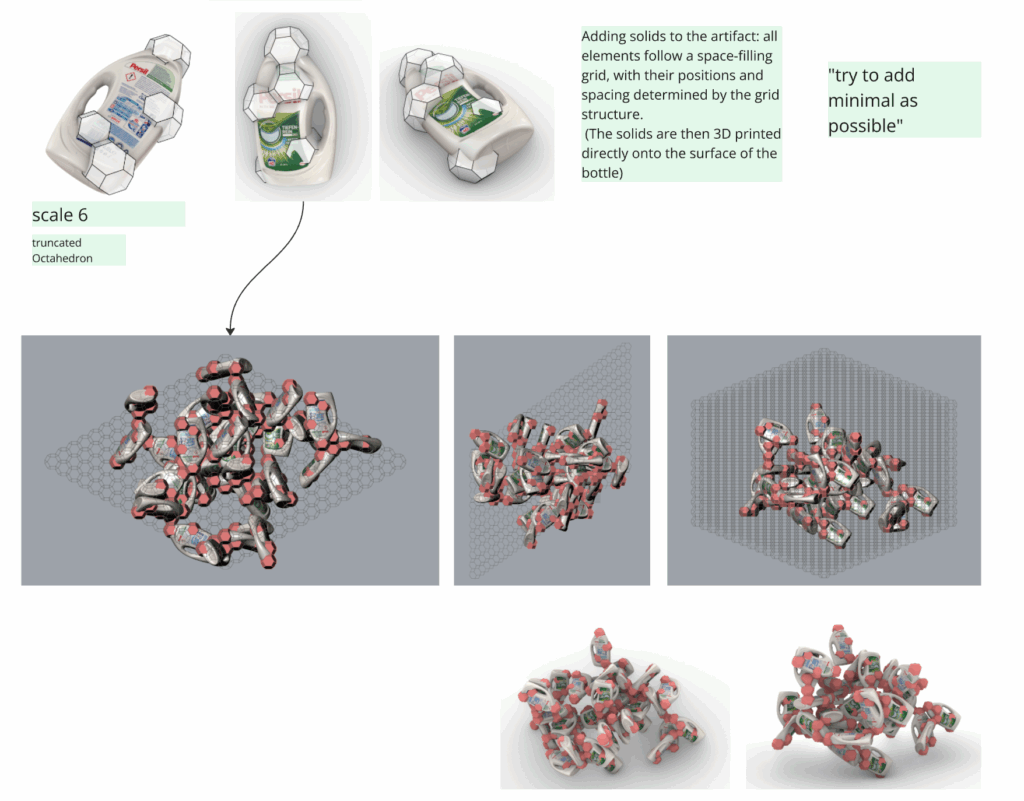


The second approach involves modifying the artefact itself. Instead of adding to it, we press the object into a mold that mirrors the geometry of the space-filling solids. The artefact becomes shaped by the system.
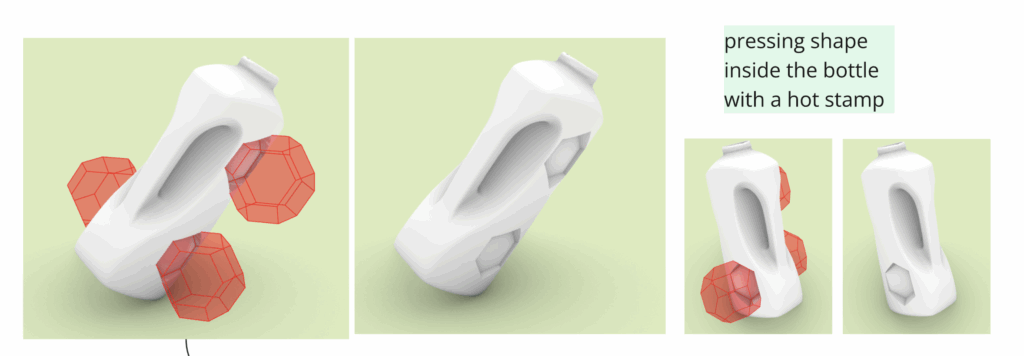
Both methods have their strengths. Adding solids preserves the original object while enabling new assembly logic. Transforming the object embeds it more fully into the system’s language. Crucially, both allow for the reuse of different artefacts within the same structural framework. This makes the system modular not just in how it assembles, but in how it adapts. By maintaining a consistent grid scale, virtually any type of waste object can be absorbed into the geometric system, unlocking new potentials for circular design.


What’s Next?
The next steps move us from digital into practice. We’re beginning real-world testing: experimenting with direct 3D printing onto waste objects, and exploring how different forms can interlock. A focus will be developing a logic for joints—how surface-to-surface connections between solids can be made secure, scalable.