Cluster 1: k-means optimization

| Lukas Allner

With specific distribution of parts, connection alignment can be optimized.

This study was part of our paper at the eCAADe conference 2025.

In continuation of previous work using k-means clustering, we used the technique to simplify an inventory of all different bicycle frames into groups of similarity, each represented by an average, or proto-part.

For this study, we parametrically generated 250 frames by interpolating geometric variations from 18 3D-scanned frames. Multidimensional feature vectors based on geometric attributes such as angles and lengths are used to create proto-parts

Exemplary sub-set of 36 frames, sorted by shape similarity using k-means clustering (above), and the representational protocol parts for each group (below).

With this modularized set, we tested whether there would be specific constellations of parts within a pattern, that would produce better connection alignment results compared to random part distribution.

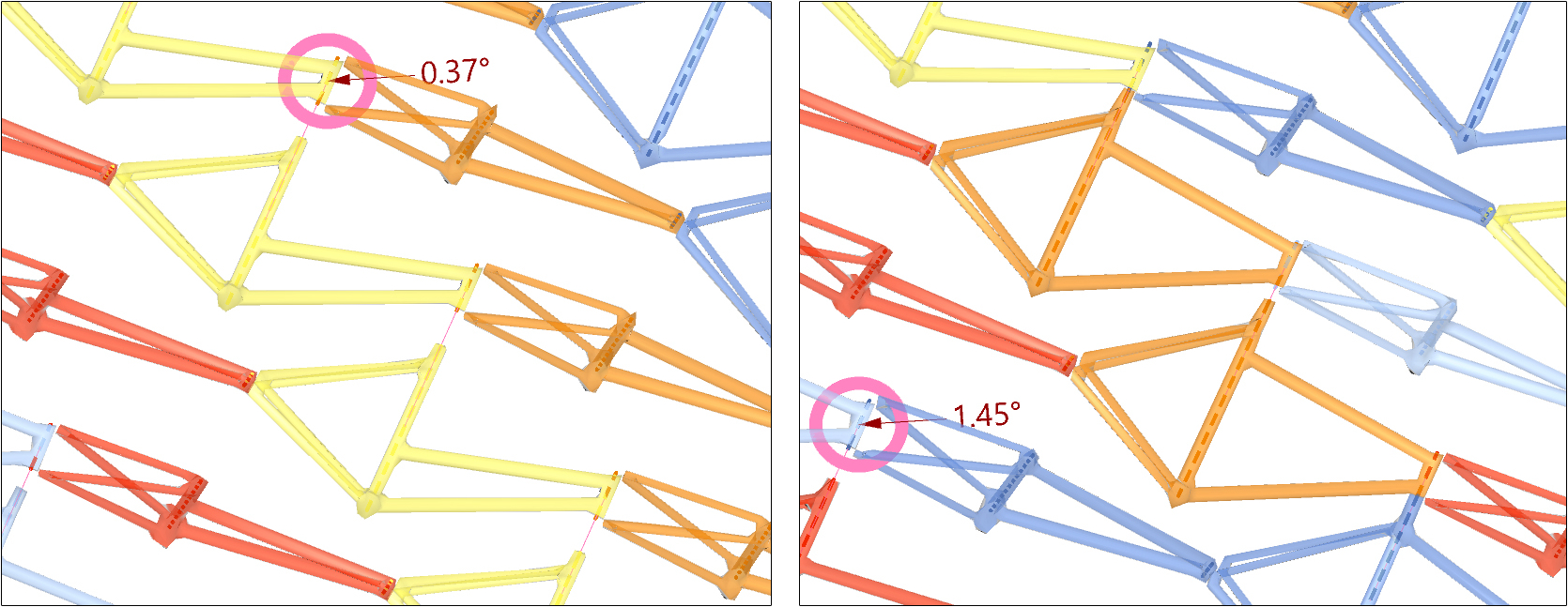
An analysis of two patterns with random part distributions showed that the largest deviations occur where frames with significantly different geometries are placed in close proximity. To address this problem, differences could be distributed evenly across the pattern, using its regularity. Both patterns are based on a periodic structure that combines linear sequences, or rows / columns into a lattice configuration. Local variations in part geometry disrupt the continuity of these sequences, leading to misalignments.

To mitigate this, instances of the same photo-parts are distributed along these linear sequences. This orderly distribution preserves the periodic pattern and reduces angular deviations at joints compared to random arrangements.

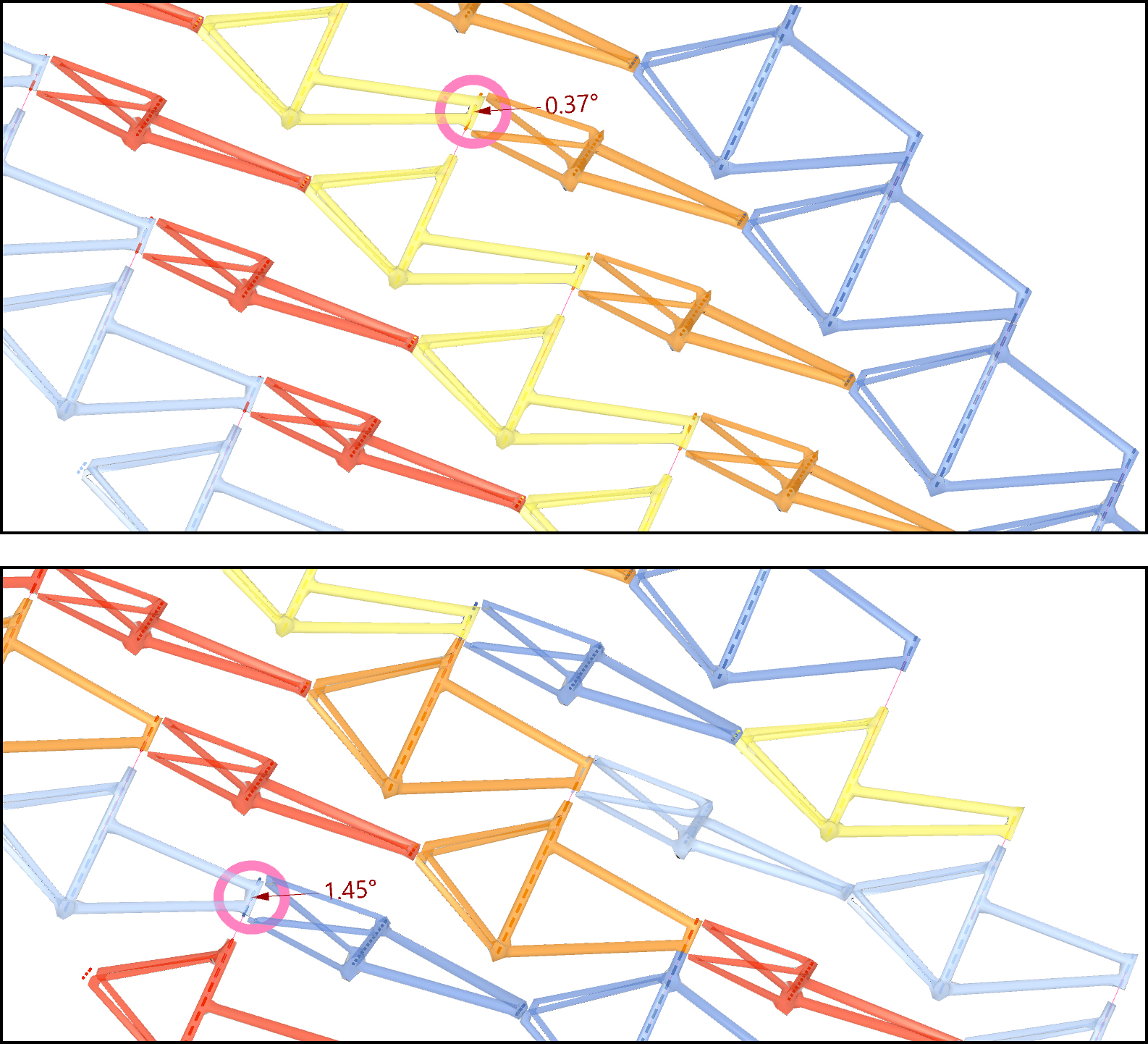
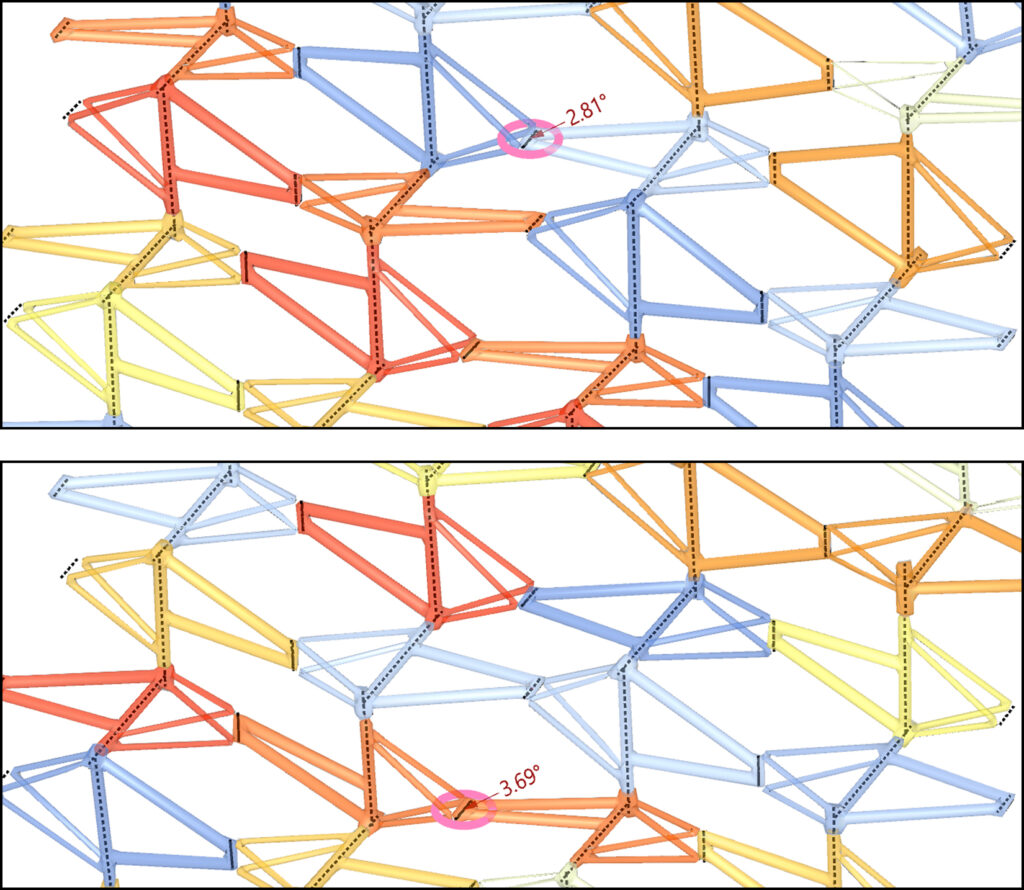
Pattern 1 / best of 50, parts sorted in rows (above), and random part distribution (below). Max. deviation highlighted
Pattern 3 / best of 50, parts sorted in rows (above), and random part distribution (below). Max. deviation highlighted

In Pattern 1, vertical rows of proto-parts tested in 50 configurations resulted in an average maximum deviation of 0.37°, compared to 1.45° for random layouts. In Pattern 3, diagonally arranged proto-parts showed 4.4° versus 5.5° in random variations.

As in previous studies, the improvements are still minimal, but consistent.

The study demonstrates that a combination of k-means clustering and orderly placement of parts according to pattern logic, offers a robust and efficient technique for optimizing part matching. It could also be translated to other material and geometry contexts and be relevant for designing with inventories of irregular parts in general, not only to assemble bicycle frames.